「スピンネットワークって何?」
「時空が粒々でできているってどういうこと?」
「量子重力理論と何の関係があるの?」
スピンネットワークは、私たちが住んでいる空間そのものが、実は連続的ではなく、目に見えない極小の「粒」でできているという驚くべき考え方です。
この概念は、1971年にイギリスの数学者・物理学者ロジャー・ペンローズによって提唱され、その後ループ量子重力理論の中心的な役割を果たすようになりました。
時空の最小単位は、プランク長(約10⁻³⁵メートル)という想像を絶する小ささで、私たちが日常で経験する滑らかな空間は、この量子的な構造を巨視的に平均化したものに過ぎません。
この記事では、スピンネットワークの基本概念から、その歴史、ループ量子重力理論での役割、そして現代物理学における意義まで、中学3年生でも理解できるように詳しく解説します。
スピンネットワークとは
スピンネットワークは、空間の量子状態を表現するための数学的な構造です。
基本的な定義
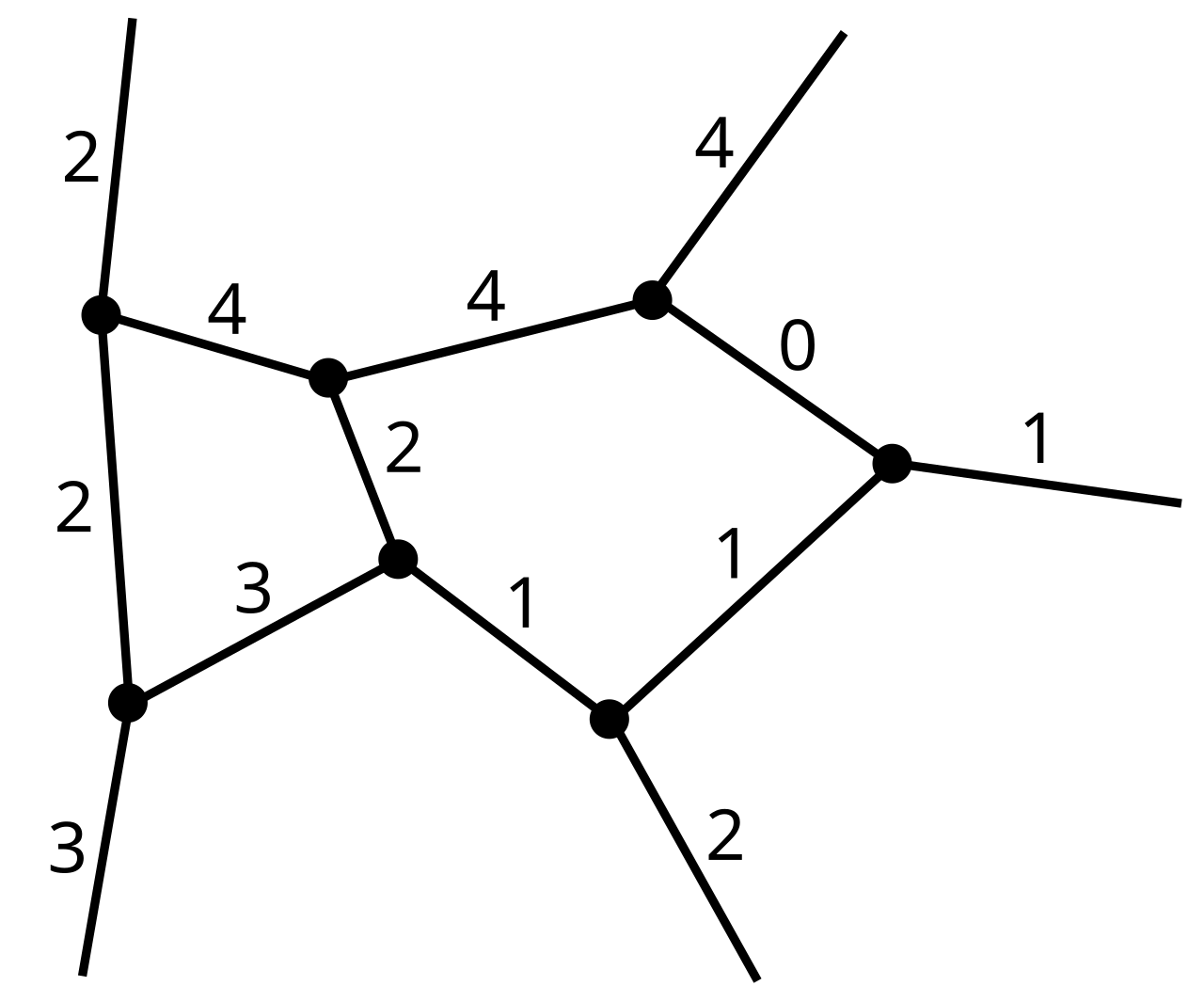
スピンネットワークは、グラフ(点と線からなる図形)の一種です。
構成要素
- ノード(節点):空間の「体積の量子」を表す点
- リンク(辺、エッジ):ノードを結ぶ線で、「面積の量子」を表す
- スピン:各リンクに付けられた数値ラベル
視覚的なイメージ
空間が「糸を織り合わせたような構造」でできていると想像してください。
- 糸の交差点がノード
- 糸そのものがリンク
- 各糸には「スピン」という情報が付いている
名前の由来
「スピン」という言葉は、量子力学で粒子の回転の性質を表す物理量から来ています。
ただし、スピンネットワークの「スピン」は、実際の回転ではなく、数学的なラベルとして使われています。
各リンクに付けられたスピン値(j = 0, 1/2, 1, 3/2, 2, …)は、そのリンクが表す面積の大きさを決定します。
何を表しているのか
スピンネットワークは、3次元空間の量子状態を表現します。
従来の物理学では、空間は連続的で滑らかなものと考えられていました。
しかし、スピンネットワークによれば、極小スケール(プランク長)では、空間は離散的な構造を持ちます。
重要な特徴
- 空間は「粒状」の構造を持つ
- 面積と体積は離散的な値しか取れない(量子化される)
- 最小の体積単位が存在する
- 空間はノードとリンクのネットワークで表現される
スピンネットワークの歴史
スピンネットワークの概念は、半世紀以上にわたる発展の歴史があります。
ロジャー・ペンローズの提唱(1971年)
ロジャー・ペンローズ(Roger Penrose, 1931年8月8日生まれ)は、イギリスの数学者・物理学者です。
2020年にノーベル物理学賞を受賞しました。
1971年の論文
ペンローズは1971年、「Angular momentum: an approach to combinatorial spacetime」という論文で、スピンネットワークを初めて提唱しました。
この論文は、ケンブリッジ大学出版局の『Quantum Theory and Beyond』という本に収録されています。
ペンローズの動機
ペンローズは、連続的な時空を仮定することから生じる物理学の困難に着目しました。
主な問題
- 量子力学では物理量が非可換(順序が重要)だが、空間座標は可換な数
- 量子計算がしばしば発散する(無限大になる)
- 重力理論の量子化が困難
これらの問題を解決するため、ペンローズは「空間が本質的に離散的である」という根本的に異なる考え方を提案しました。
初期のスピンネットワーク
ペンローズの最初のスピンネットワークは、次のように定義されました。
- 各線分は「単位」(素粒子または複合系)の世界線を表す
- 各頂点で3本の線分が結合する
- 頂点は、1つの単位が2つに分裂するか、2つが1つに結合する事象を表す
- すべての線分が頂点で結合されたものを「閉じたスピンネットワーク」と呼ぶ
ループ量子重力理論での再発見(1988-1994年)
ペンローズの提唱から約20年後、スピンネットワークは思いがけない形で再登場します。
カルロ・ロヴェッリとリー・スモーリン(1988-1990年)
イタリアの物理学者カルロ・ロヴェッリ(Carlo Rovelli)とアメリカの物理学者リー・スモーリン(Lee Smolin)は、一般相対性理論を量子化する研究を進めていました。
彼らは、ループ(閉じた経路)を基本的な変数として使う「ループ表現」を開発しました。
驚くべき発見
1988年から1990年にかけて、ロヴェッリとスモーリンは、量子幾何学の状態の明示的な基底を構築しました。
そして驚くべきことに、この基底状態はペンローズのスピンネットワークと全く同じ数学的構造を持っていたのです。
ペンローズは直感だけに基づいて提唱しましたが、厳密な量子化手続きから自然にスピンネットワークが現れたのです。
1994年の画期的な結果
1994年、ロヴェッリとスモーリンは、面積と体積を表す量子演算子が離散的なスペクトル(固有値)を持つことを示しました。
これは、面積と体積が連続的な値ではなく、飛び飛びの値しか取れないことを意味します。
1995年の重要論文
1995年5月4日、ロヴェッリとスモーリンは「Spin Networks and Quantum Gravity」という論文をarXivに投稿しました(論文番号:gr-qc/9505006)。
この論文は、Physical Review D誌の52巻(1995年)に掲載され、ループ量子重力理論におけるスピンネットワークの基礎を確立しました。
その後の発展
1990年代後半から2000年代
- スピンフォーム(時間発展を含む)理論の発展
- ブラックホールエントロピーの計算
- ループ量子宇宙論の構築
- 数値シミュレーション技術の進歩
主要な研究者たち
- カルロ・ロヴェッリ(イタリア)
- リー・スモーリン(アメリカ)
- アベイ・アシュテカール(インド系アメリカ人)
- トーマス・ティーマン(ドイツ)
- ホルヘ・プリン(アルゼンチン系アメリカ人)
- ロドルフォ・ガンビーニ(ウルグアイ)
ループ量子重力理論
スピンネットワークは、ループ量子重力理論(Loop Quantum Gravity, LQG)の中心的な概念です。
ループ量子重力理論とは
ループ量子重力理論は、量子力学と一般相対性理論を統合しようとする理論です。
目標
重力を含むすべての物理現象を、量子力学と整合的に記述する理論を作る。
超弦理論との違い
量子重力理論には、ループ量子重力理論のほかに超弦理論(または超ひも理論)があります。
超弦理論
- 時空は背景として最初から存在すると仮定(背景依存)
- 10次元または11次元の高次元時空を必要とする
- 超対称性を仮定
- すべての素粒子と相互作用を統一
ループ量子重力理論
- 時空は背景として存在せず、理論自身が時空を決定(背景独立)
- 4次元時空を基礎とする
- 超対称性を仮定しない
- 重力の量子化に焦点
背景独立性
ループ量子重力理論の最も重要な特徴の一つが、背景独立性です。
背景独立とは
時空そのものが動的に変化し、固定された「舞台」として存在しないこと。
一般相対性理論では、時空は物質とエネルギーによって曲がります。
ループ量子重力理論は、この性質を量子論のレベルでも保つことを目指しています。
従来の場の量子論
電磁気力、弱い力、強い力を記述する標準模型では、あらかじめ固定された平坦な時空(ミンコフスキー時空)の上で量子場を定義します。
しかし、重力理論では時空自体が動的なので、この方法は使えません。
時空の離散構造
ループ量子重力理論によれば、時空は極小スケールで離散的な構造を持ちます。
プランク長とプランク時間
- プランク長:ℓₚ ≈ 1.6 × 10⁻³⁵ メートル
- プランク時間:tₚ ≈ 5.4 × 10⁻⁴⁴ 秒
これらは、長さと時間の自然な最小単位です。
最小体積
空間の最小体積は、約1立方プランク長、つまり約10⁻⁹⁹ cm³です。
これは想像を絶する小ささです。
比較
- 原子核のサイズ:約10⁻¹³ cm
- 原子のサイズ:約10⁻⁸ cm
- プランク長:約10⁻³³ cm
プランク長は、原子核よりもさらに20桁も小さいのです。
スピンネットワークの役割
ループ量子重力理論では、スピンネットワークは3次元空間の量子状態を表します。
グラフの構造
- ノード:空間の「点」ではなく、「体積の量子」
- リンク:ノードを結ぶ線で、「面積の量子」を表す
- スピン値:各リンクに付けられた数値(j = 0, 1/2, 1, 3/2, 2, …)
面積の量子化
任意の2次元面を横切るリンクのスピン値 j から、その面の面積が計算できます。
面積の固有値
A = 8πγ ℓₚ² Σ √[j(j+1)]
- γ:バルベロ=イミルツィ・パラメータ(約0.2375)
- ℓₚ:プランク長
- j:面を横切る各リンクのスピン
- Σ:すべてのリンクにわたる和
この式から、面積が離散的な値しか取れないことがわかります。
体積の量子化
同様に、3次元領域の体積も離散的です。
各ノードが「体積の量子」に対応し、領域の体積はその中のノードからの寄与の和になります。
スピンフォーム
スピンネットワークに時間の要素を加えたものが、スピンフォーム(Spin foam、スピンの泡)です。
スピンネットワークからスピンフォームへ
スピンネットワーク
3次元空間の量子状態を表す静的な構造。
スピンフォーム
4次元時空の量子状態を表す動的な構造。
構造の変化
スピンネットワークに時間次元を加えると、以下のように変化します。
1次元が2次元に
- リンク(1次元の線)→ 面(2次元の広がり)
- ノード(0次元の点)→ リンク(1次元の線)
時間発展
スピンネットワークの状態が時間とともに変化する様子が、スピンフォームで表現されます。
具体的には、スピンフォームの中で線と線がノードで合体することによって、スピンネットワークの遷移が表現されます。
プランク時間ごとの離散的変化
ループ量子重力理論では、時間の流れも連続的ではありません。
離散的な時間
時空は、プランク時間(約10⁻⁴⁴秒)という極めて短い時間間隔で、離散的に変化します。
時計の比喩
無数の時計が、プランク時間ごとに一斉にカチカチと時を刻むイメージです。
時間の問題
ループ量子重力理論では、「時間」の扱いが非常に深遠で難しい問題です。
時間は含まれていない?
基本方程式(ハミルトン制約)には、時間が明示的に現れません。
これは「時間は基本的なものではない」ことを示唆しています。
時間の出現
私たちが経験する「時間の流れ」は、スピンネットワークの変化や、物事の推移を観察することで初めて認識されるものかもしれません。
これは、現象学という哲学理論に通じる考え方です。
スピンネットワークの数学的性質
スピンネットワークには、興味深い数学的性質があります。
ノルム(規範)
任意の閉じたスピンネットワークに対して、非負の整数であるノルムを計算できます。
ノルムは、そのスピンネットワークの生起確率に関連しています。
ノルムがゼロのネットワークは、生起確率がゼロです。
三角不等式とフェルミオン保存
スピンネットワークが非ゼロのノルムを持つためには、各頂点で以下の条件を満たす必要があります。
3つのスピン a, b, c を持つリンクが頂点で結合する場合
条件1:三角不等式
- a ≤ b + c
- b ≤ a + c
- c ≤ a + b
条件2:フェルミオン保存
a + b + c は偶数でなければならない。
例
- a = 3, b = 4, c = 6 は不可能(3 + 4 + 6 = 13は奇数)
- a = 3, b = 4, c = 9 は不可能(9 > 3 + 4)
- a = 3, b = 4, c = 5 は可能(3 + 4 + 5 = 12は偶数、三角不等式も満たす)
インタートワイナー
頂点では、複数のリンクのスピンを適切に結合させる必要があります。
この結合規則をインタートワイナー(intertwiner)と呼びます。
インタートワイナーは、SU(2)群(2次元ユニタリ行列の群)の表現論に基づいて構成されます。
ゲージ不変性
スピンネットワークは、ゲージ変換(局所的な変換)に対して不変です。
これは、物理的に意味のある状態を選び出すための重要な性質です。
ループ量子重力理論の成果
スピンネットワークを基礎とするループ量子重力理論は、いくつかの重要な成果を上げています。
1. ブラックホールエントロピー
ループ量子重力理論は、ブラックホールのエントロピーを微視的に説明することに成功しました。
ベッケンシュタイン=ホーキングの公式
S = (k c³ / 4ℏG) A
- S:ブラックホールのエントロピー
- A:事象の地平面の面積
- k:ボルツマン定数
- c:光速
- ℏ:プランク定数(換算プランク定数)
- G:万有引力定数
この公式は、ブラックホールのエントロピーが地平面の面積に比例することを示しています。
ループ量子重力理論による説明
事象の地平面を横切るスピンネットワークのリンクの数を数えることで、ブラックホールのエントロピーが計算できます。
これは、エントロピーが微視的な量子状態の数に由来することを示しています。
2. ビッグバン特異点の回避
古典的な一般相対性理論の問題
一般相対性理論によれば、宇宙の始まり(ビッグバン)では、密度と曲率が無限大になる「特異点」が存在します。
ループ量子宇宙論(LQC)
ループ量子重力理論を簡略化した宇宙論モデルであるループ量子宇宙論では、この問題が解決されます。
ビッグバウンス
量子効果により、ビッグバン特異点は「ビッグバウンス」(大きな跳ね返り)に置き換えられます。
つまり、私たちの宇宙は特異点から始まったのではなく、収縮していた以前の宇宙が跳ね返って膨張し始めた可能性があります。
3. 紫外発散の回避
量子場の理論では、極端に短い距離(高エネルギー)での計算が発散する「紫外発散」という問題があります。
ループ量子重力理論では、プランク長という最小長さが存在するため、この問題が自然に回避されます。
ループ量子重力理論の課題
スピンネットワークとループ量子重力理論には、まだ解決されていない重要な課題があります。
1. 低エネルギー極限との接続
問題
プランクスケールでの理論構造は明確ですが、私たちが観測できる低エネルギー(マクロスケール)での物理とどう接続するかが課題です。
連続極限
離散的なスピンネットワークから、滑らかな連続的時空をどのように再構築するかは、重要な未解決問題です。
2. 動力学の確立
ハミルトン制約の問題
ハミルトン制約(時間発展を記述する方程式)を厳密に解くことは、非常に困難です。
1996年にトーマス・ティーマンが数学的に厳密な定式化を与えましたが、その物理的解釈や計算可能性には課題が残っています。
3. 実験的検証の困難さ
観測不可能な領域
プランクスケール(10⁻³⁵メートル)は、現在の技術では直接観測できません。
間接的な検証の可能性
- ガンマ線バーストの観測:遠方の宇宙で発生したガンマ線バーストの光が、波長によってわずかな時間差で地球に届く可能性
- 宇宙マイクロ波背景放射:初期宇宙のゆらぎへの量子重力効果
- ブラックホール蒸発:ブラックホールが完全に蒸発する最終段階での量子効果
4. 標準模型との統合
ループ量子重力理論は、重力の量子化に焦点を当てています。
しかし、電磁気力、弱い力、強い力を記述する標準模型をどのように取り込むかは、まだ完全には解決されていません。
超弦理論は、すべての相互作用を統一することを目指していますが、ループ量子重力理論は異なるアプローチを取っています。
スピンネットワークの意義
スピンネットワークは、現代物理学に重要な示唆を与えています。
1. 時空の本質への洞察
スピンネットワークは、「時空とは何か」という根本的な問いに新しい答えを提供します。
従来の見方
時空は連続的で滑らかな「容器」であり、物質とエネルギーはその中で運動する。
スピンネットワークの見方
時空は、量子的な関係性のネットワークであり、連続性は幻想である。
2. 情報理論的視点
スピンネットワークは、量子情報理論と深く関連しています。
ブラックホールのエントロピーが情報量に関係していることは、時空と情報が根本的に結びついている可能性を示唆しています。
3. 創発的時空
スピンネットワークの集団的な振る舞いから、マクロな時空が「創発」する可能性があります。
これは、水の分子から流体力学が創発するように、微視的な量子構造から古典的な時空が現れるという考え方です。
4. 量子重力理論への道筋
スピンネットワークは、量子力学と一般相対性理論を統合する具体的な数学的枠組みを提供します。
まだ完成には至っていませんが、重要な一歩であることは間違いありません。
関連する概念
スピンネットワークは、他の物理学・数学の概念とも関連しています。
1. 結び目理論
スピンネットワークは、結び目理論(knot theory)と深い関係があります。
スピンネットワークを使って、ジョーンズ多項式などの結び目不変量を構成できます。
2. 群の表現論
スピンネットワークの数学的基礎は、群の表現論(特にSU(2)群)です。
量子力学の角運動量理論と本質的に同じ数学が使われています。
3. トポロジカル場の理論
スピンネットワークは、トポロジカル場の理論(特にチャーン=サイモンズ理論)とも関連しています。
4. 群場理論
最近の研究では、群場理論(Group Field Theory)という、スピンネットワークをさらに一般化した枠組みも発展しています。
まとめ
スピンネットワークと量子重力理論について解説しました。
スピンネットワークとは
- 点(ノード)と線(リンク)からなるグラフ構造
- 3次元空間の量子状態を表現
- 各リンクにはスピンという数値ラベルが付く
- ノードは「体積の量子」、リンクは「面積の量子」を表す
歴史
- 1971年:ロジャー・ペンローズが提唱
- 1988-1990年:カルロ・ロヴェッリとリー・スモーリンがループ量子重力理論に適用
- 1994年:面積と体積演算子の離散スペクトルを発見
- 1995年:重要論文「Spin Networks and Quantum Gravity」発表
ループ量子重力理論
- 量子力学と一般相対性理論を統合する理論
- 背景独立(時空そのものが動的)
- 4次元時空を基礎とする
- プランク長(10⁻³⁵m)が最小単位
- 超弦理論とは異なるアプローチ
時空の離散構造
- 最小長さ:プランク長 ≈ 1.6 × 10⁻³⁵ メートル
- 最小時間:プランク時間 ≈ 5.4 × 10⁻⁴⁴ 秒
- 最小体積:約1立方プランク長 ≈ 10⁻⁹⁹ cm³
- 面積と体積は離散的な値しか取れない
スピンフォーム
- スピンネットワークに時間要素を加えたもの
- 4次元時空の量子状態を表現
- スピンネットワークの時間発展を記述
- プランク時間ごとに離散的に変化
数学的性質
- ノルム(規範)の計算
- 三角不等式とフェルミオン保存則
- インタートワイナー(頂点での結合規則)
- ゲージ不変性
主な成果
- ブラックホールエントロピー:地平面の面積に比例するエントロピーを微視的に説明
- ビッグバン特異点の回避:ビッグバウンスによる宇宙の起源
- 紫外発散の回避:最小長さの存在により発散を回避
課題
- 低エネルギー極限との接続
- 動力学の確立
- 実験的検証の困難さ
- 標準模型との統合
意義
- 時空の本質への新しい洞察(時空は離散的)
- 情報理論的視点(時空と情報の結びつき)
- 創発的時空(微視的構造から古典的時空が現れる)
- 量子重力理論への具体的な道筋
スピンネットワークは、1971年にペンローズが直感的に提唱した概念が、20年後に厳密な量子化手続きから自然に現れるという、物理学における美しい発見の一つです。
私たちが住んでいる空間が、実は極小のネットワーク構造でできているという考え方は、古代ギリシャの原子論を思い起こさせますが、それをはるかに超える精密な数学的構造を持っています。
ループ量子重力理論とスピンネットワークは、まだ発展途上の理論ですが、量子力学と一般相対性理論を統合し、「時空とは何か」という根本的な問いに答えようとする、現代物理学の最前線の研究です。
参考情報
- Wikipedia – Spin network
![]() Spin network - Wikipedia
Spin network - Wikipedia - Wikipedia – Loop quantum gravity
![]()
![]()
 Loop quantum gravity - Wikipedia
Loop quantum gravity - Wikipedia - Wikipedia – History of loop quantum gravity
History of loop quantum gravity - Wikipedia
- Wikipedia – ループ量子重力理論 [https://ja.wikipedia.org/wiki/ループ量子重力理論]
- 日経サイエンス – 時空の原子を追うループ量子重力理論
![]()
![]()
 時空の原子を追うループ量子重力理論|日経サイエンス私たちは空間も時間も連続したものだと考えているが,実は大間違いかもしれない。相対論と量子力学の統合を目指す新理論によると,「時空の原子」が存在する。アインシュタインが果たせなかった難問解決の道筋が見えてきた。 空間の構 … 続きを読む →
時空の原子を追うループ量子重力理論|日経サイエンス私たちは空間も時間も連続したものだと考えているが,実は大間違いかもしれない。相対論と量子力学の統合を目指す新理論によると,「時空の原子」が存在する。アインシュタインが果たせなかった難問解決の道筋が見えてきた。 空間の構 … 続きを読む → - arXiv – Spin Networks and Quantum Gravity (Rovelli & Smolin, 1995)
Spin Networks and Quantum GravityWe introduce a new basis on the state space of non-perturbative quantum gravity. The states of this basis are linearly i...
- note – ループ量子重力理論のほのかな香りを楽しむ
![]()
![]()
 ループ量子重力理論のほのかな香りを楽しむ|福岡 浩二前回の投稿で、超ひも理論に次ぐもう1つの量子重力理論候補「ループ量子重力理論」の違いだけ触れました。 忘れないうちに、「ループ量子重力理論」についてその香りをかぎ取れる程度に紹介しておきます。 改めてですが、量子力学と一般相対性理論を統合す...
ループ量子重力理論のほのかな香りを楽しむ|福岡 浩二前回の投稿で、超ひも理論に次ぐもう1つの量子重力理論候補「ループ量子重力理論」の違いだけ触れました。 忘れないうちに、「ループ量子重力理論」についてその香りをかぎ取れる程度に紹介しておきます。 改めてですが、量子力学と一般相対性理論を統合す... - note – ループ量子重力について
![]()
![]()
 ループ量子重力について|かえる1. 背景と動機 (1) 一般相対性理論の量子化問題: アインシュタインの一般相対性理論は重力を時空の幾何学的性質として記述する傑出した理論であるが、これは古典的な連続理論であり、量子力学との整合的な統一が難題となっている。場の量子論におい...
ループ量子重力について|かえる1. 背景と動機 (1) 一般相対性理論の量子化問題: アインシュタインの一般相対性理論は重力を時空の幾何学的性質として記述する傑出した理論であるが、これは古典的な連続理論であり、量子力学との整合的な統一が難題となっている。場の量子論におい... - Oxford Mathematics – Carlo Rovelli Lecture on Spin Networks
Carlo Rovelli - Spin networks: the quantum structure of spacetime from Penrose's intuition to Loop Quantum Gravity | Mathematical Institute
- Hamilton College – A Spin Network Primer (Seth A. Major) https://academics.hamilton.edu/physics/smajor/courses/320Info/sn.pdf







コメント