🎯 この記事で分かること
- なぜ連続な関数には必ず最大値と最小値があるの?
- どんな条件が必要なの?
- 私たちの生活にどう役立ってるの?
📖 はじめに:山には必ず頂上がある理由
みなさん、山登りを想像してみてください。
山の道が途切れることなく続いていて、しかも山の範囲が決まっていれば、必ず頂上(最高点)と一番低い場所(最低点)がありますよね?
実は数学でも、これと同じことが言えるんです!
これが今回お話しする「ワイエルシュトラスの最大値定理」の中身なんですよ。
なぜこれが大切なの?
この定理があるおかげで:
- 🌉 橋の設計者は、橋にかかる最大の力を計算できます
- 💰 お店の経営者は、最適な商品の値段を見つけられます
- 🤖 AIエンジニアは、機械学習を効率よく進められます
つまり、「答えが必ずある」という保証があるから、安心して答えを探せるんです。
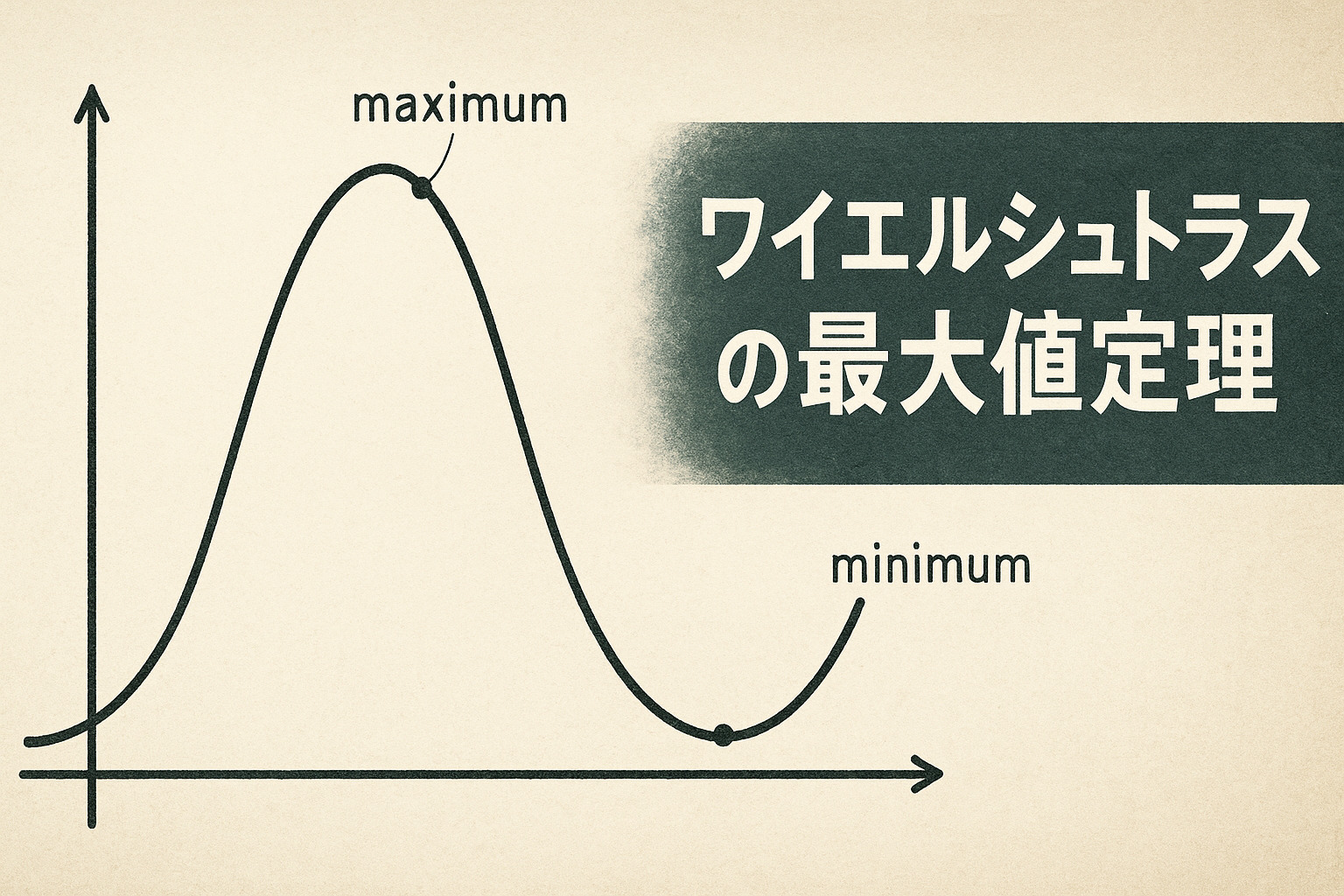
🏔️ グラフの頂点は必ず見つかる!定理の基本を知ろう

定理を簡単に言うと?
「なめらかな線(連続な関数)が、決まった範囲の中にあるなら、必ず一番高い点と一番低い点がある」
これだけです!シンプルでしょう?
具体例で見てみよう
たとえば、放物線(ボールを投げた時の軌道みたいな曲線)を考えてみましょう。
y = x² という関数を、x = -2 から x = 3 の範囲で見るこの場合:
- 📊 最小値:x = 0 のとき、y = 0(一番低い点)
- 📈 最大値:x = 3 のとき、y = 9(一番高い点)
ちゃんと最高点と最低点がありますよね!
なぜこれが革命的なの?
実は、昔の数学者たちは「答えがあるかどうか分からない問題」に悩まされていました。
でも、この定理のおかげで:
- ✅ まず「答えは必ずある」と分かる
- ✅ だから安心して「どこに答えがあるか」を探せる
これって、宝の地図に「宝は必ずある」って書いてあるようなものです。探す価値があると分かっているから、頑張れますよね!
⚠️ 3つの絶対条件:1つでも欠けたらアウト!
定理が成り立つには、3つの条件が全部そろう必要があります。
条件1:連続性(線がつながっていること)
グラフに穴や切れ目があったらダメなんです。
❌ ダメな例
f(x) = 1/x (xが0のとき定義できない)この関数は、x = 0 で無限大に飛んでいってしまいます。グラフに穴が開いているイメージですね。
⭕ 良い例
f(x) = x² (どこでもなめらかにつながっている)条件2:閉区間(両端を含むこと)
範囲の両端まできちんと含める必要があります。
❌ ダメな例:開区間 (0, 1)
- 0に近づけるけど、0は含まない
- 1に近づけるけど、1は含まない
- だから最大値も最小値も「取りそうで取らない」状態に!
⭕ 良い例:閉区間 [0, 1]
- 0も1も含む
- だから逃げ場がない!
条件3:有界性(範囲が無限じゃないこと)
無限に広がる範囲はダメです。
❌ ダメな例
区間 [0, ∞) で f(x) = x を考えるxがどんどん大きくなれば、f(x)も無限に大きくなっちゃいます。最大値なんて存在しません!
⭕ 良い例
区間 [0, 100] で f(x) = x を考える範囲が決まっているから、最大値は100で確定!
3つの条件をまとめると
「なめらかで」「両端まで含んで」「範囲が決まってる」
この3つがそろえば、必ず最大値と最小値があるんです!
🧪 実際に試してみよう!成功例と失敗例
✅ 成功例1:上に凸の放物線
f(x) = -x² + 4 を区間 [-3, 3] で考える- 連続? → ⭕ どこでもなめらか
- 閉区間? → ⭕ 両端含む
- 有界? → ⭕ 範囲が決まってる
結果:
- 最大値4(x = 0のとき)
- 最小値-5(x = ±3のとき)
✅ 成功例2:波のような三角関数
f(x) = sin(x) を区間 [0, 2π] で考えるサインカーブって、波のように上下しますよね。
- 連続? → ⭕
- 閉区間? → ⭕
- 有界? → ⭕
結果:
- 最大値1(波の頂上)
- 最小値-1(波の谷底)
❌ 失敗例1:区間に穴がある
f(x) = 1/x を開区間 (0, 1) で考える- x = 0 に近づくと → 無限大に発散!
- 最大値が存在しない…
❌ 失敗例2:範囲が無限
f(x) = arctan(x) を (-∞, ∞) で考える- いくら頑張っても、決して π/2 には届かない
- 最大値も最小値も「取りそうで取らない」
🌟 実生活での活用例:意外と身近な定理

🏗️ 橋の設計
橋を作るとき、エンジニアさんは考えます:
「この橋にかかる最大の力はどれくらい?」
- 荷重(重さ)は連続的に変化する
- 設計パラメータには現実的な範囲がある
- だから必ず「最悪のケース」が存在する!
この定理があるから、最悪のケースに耐えられる橋を設計できるんです。
💰 お店の価格設定
コンビニの店長さんが考えること:
「おにぎりをいくらで売れば一番儲かる?」
- 価格は連続的に変えられる(100円、101円、102円…)
- 現実的な価格範囲がある(50円〜300円とか)
- だから必ず「最適な価格」が存在する!
🤖 AIの機械学習
AIを賢くするとき:
「誤差を一番小さくする設定は?」
- パラメータは連続的に調整できる
- 調整範囲には限界がある
- だから必ず「最適な設定」が見つかる!
🚚 配送ルートの最適化
宅配便の会社が考えること:
「一番短いルートはどれ?」
- 距離は連続的に変化
- 可能なルートには限りがある
- だから必ず「最短ルート」が存在する!
🧠 もう少し深く:コンパクト性という魔法の概念
コンパクトって何?
簡単に言うと、「閉じていて、かつ範囲が決まっている」ことです。
つまり:
- 逃げ場がない(閉じている)
- どこまでも行けない(有界)
この2つの性質があると、とても扱いやすいんです。
なぜコンパクトが大切?
「連続な関数は、コンパクトな集合をコンパクトな集合に変換する」
という、もっと一般的な法則があるんです。
これを使うと:
- 区間 [a, b] はコンパクト
- 連続関数で変換してもコンパクト
- コンパクトなら最大値・最小値がある
という流れで、定理が証明できちゃうんです!
👨🔬 定理の父:カール・ワイエルシュトラス物語
苦労人の数学者
カール・ワイエルシュトラス(1815-1897)は、実はすごく苦労した人でした。
- 😔 若い頃:お父さんに法律を勉強しろと言われた
- 📚 でも本当は:数学が大好きで、こっそり独学
- 👨🏫 結果:大学を卒業できず、中学校の先生に…
大逆転の人生
でも、40歳のとき転機が!
- 🎉 素晴らしい論文を発表
- 🏆 名誉博士号をゲット
- 👨🎓 ベルリン大学の教授に!
何がすごかったの?
ワイエルシュトラスは「数学を厳密にした人」として有名です。
それまでの数学:
- 「だいたいこんな感じ」
- 「図を見れば分かるでしょ?」
ワイエルシュトラスの数学:
- 「論理的に完璧に証明する」
- 「曖昧さは一切許さない」
この厳密さが、現代数学の基礎になったんです!
📝 まとめ:確実性という最高の贈り物
この定理が教えてくれること
「条件さえ整えば、答えは必ずある」
これって、すごく安心できることじゃないですか?
3つの条件をもう一度
- 連続性(なめらかにつながっている)
- 閉区間(両端を含む)
- 有界性(範囲が決まっている)
この3つがそろえば、最大値と最小値は必ず存在します!
なぜ大切なの?
- 🎯 問題を解く前に、解があることが分かる
- 💪 だから自信を持って、解を探せる
- 🔧 工学から経済まで、幅広く活用できる
最後に
ワイエルシュトラスの最大値定理は、数学が私たちに与えてくれる「確実性」という贈り物です。
橋を設計するときも、AIを作るときも、お店の経営をするときも、この定理が陰で支えてくれているんですね。
数学って、意外と身近で頼もしい味方だと思いませんか?
🤔 よくある質問
Q: 連続じゃない関数でも、最大値・最小値があることはある?
A: はい、あることもあります!でも「必ず」とは言えないんです。定理の価値は「必ず存在する」という保証にあります。
Q: 実際に最大値を見つけるにはどうすればいい?
A: 微分を使って探すのが一般的です。定理は「存在する」ことを保証し、微分は「どこにあるか」を教えてくれます。
Q: もっと複雑な関数でも成り立つ?
A: はい!多変数関数(3次元以上)でも、条件を満たせば成り立ちます。